『僅かな違いで好きになる~コンパス&九九しりとり~』(5年生 算数)
5年生の算数では【正多角形と円】の学習をしています。単元の導入では、コンパスを使って模様づくりを行いました。

今日で4時間目だったので、コンパスをうまく使えるようになってきましたが、微細な運動が苦手な子は少なくなりません。問題集を解くだけでなく、こういった作業を多くやらせてあげたいと毎年強く感じます。

子供たちのコンパスをよく見てみると持ち手の部分にキャップのようなものがついていて回しやすくなっているタイプや持ち手の部分が太くなっているタイプなど今は様々なものがあります。私も実際に使ってみましたが、回しやすいです!見た目はほとんど同じでも一つ一つに僅かな違いがあり、その僅かな違いで算数を好きになったり、算数が得意になったりするかもしれないなと感じました。やはり使う道具は大切です。

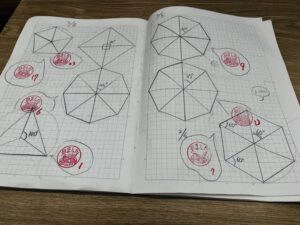
次に、半径4㎝の円の中に正三角形、正方形と描いていきました。しばらくすると、「あれ?だんだん円に近づいていない?」という声が聞こえてきました。

円周は直径の3.14倍です。この公式をほとんどの子が知っています。しかし、なぜ3.14倍になるのかは理解していない子が多く、この意味を説明して分かった時の子供たちの表情はとても良かったです。こうなると面白いです。こちらが何も言わなくても「正五角形を描いてみたい!」「正六角形は25.12㎝に近づくかな?」と次々に試してみたいという子が出てきます。あとは見守るだけといった時間が作り出せました。
最後に、図形領域など思考力が試される単元だと、どうしても45分で解く問題数が少なくなってしまいます。そこで、授業の最初の5分間は『九九しりとり』を行っています。『九九しりとり』は、2×7=14と答えたら、次は4から始まる九九を行うというものです。例えば、2×7=14→4×8=32→2×9=18、、、といった具合です。このゲームのルールは2つあります。❶最後が0はダメです。普通のしりとりの『ん』に該当します。(10、20、30、40)❷同じ答えはダメです。


『九九しりとり』はみんな大好きで、授業開始のチャイム前から夢中で取り組んでいます!開始して2週間ほどですが、このゲームを通して奇数偶数の数の仕組みを掴み、ほとんどの子が5分間で20ポイントを超えられるようになりました。





何がきっかけで算数好きになるかは分かりません。教員自身も楽しみながら授業に算数が好きになる色々な仕掛けを入れていきたいと思います。まずは、相棒となる道具を大切にしましょう!(自分に合うものが見つかると良いですね。)そして、ゲームで楽しむというのも良いと思います!
※現在、『九九しりとり』5年生最高記録は27ポイントです。5年生でなくても九九を習った子なら誰でもできると思います。ぜひ挑戦してみてください!



